Credit Risk Modeling in Python
bestseller

Name: Credit Risk Modeling in Python Course
Price: 36 USD

4.9/5

(412)

Blend credit risk modeling skills with Python programming: Learn how to estimate a bank’s loan portfolio's expected loss

8 hours of content 9786 students

Start for Free

What you get:

8 hours of content
80 Interactive exercises
119 Downloadable resources
World-class instructor
Closed captions
Q&A support
Future course updates
Course exam
Certificate of achievement

Credit Risk Modeling in Python
bestseller

A course by Nikolay Georgiev

Start for Free

What you get:

8 hours of content
80 Interactive exercises
119 Downloadable resources
World-class instructor
Closed captions
Q&A support
Future course updates
Course exam
Certificate of achievement

$99.00

Lifetime access

Buy now

Start for Free

What you get:

8 hours of content
80 Interactive exercises
119 Downloadable resources
World-class instructor
Closed captions
Q&A support
Future course updates
Course exam
Certificate of achievement

What You Learn

Expand your business acumen with deep understanding of retail banking processes and identifying key value drivers
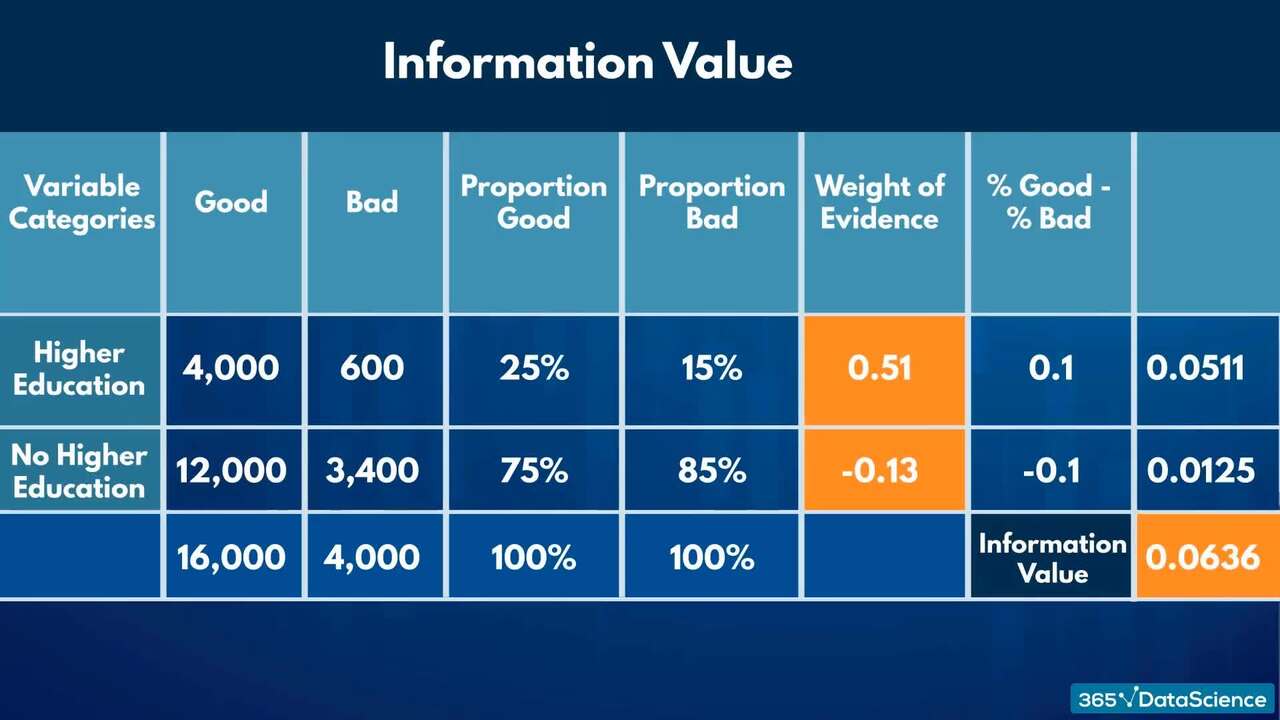
Gain comprehensive credit risk modeling knowledge, including concepts such as Basel II, probability of default (PD), loss given default (LGD), and exposure at default (EAD)
Apply logistic regression in Python to predict credit risk
Boost your data pre-processing skills by cleaning real-life loan portfolio data
Acquire specialized credit risk modeling skills and differentiate your data scientist resume
Secure a competitive edge over other candidates when applying for retail banking data scientist roles

Top Choice of Leading Companies Worldwide

Industry leaders and professionals globally rely on this top-rated course to enhance their skills.

Course Description

Credit risk modeling is the place where data science and fintech meet. It is one of the most important activities conducted in a bank, with the most attention since the recession. At present, it is the only comprehensive credit risk modeling course in Python available online – taking you from preprocessing, through probability of default (PD), loss given default (LGD) and exposure at default (EAD) modeling, all the way to calculating expected loss (EL).

Learn for Free

1.1 What does the course cover

5 min

1.2 What is credit risk and why is it important?

5 min

1.3 Expected loss (EL) and its components: PD, LGD and EAD

4 min

1.4 Capital adequacy, regulations, and the Basel II accord

5 min

1.5 Basel II approaches: SA, F-IRB, and A-IRB

10 min

1.6 Different facility types (asset classes) and credit risk modeling approaches

9 min

Curriculum

1. Introduction

6 Lessons 38 Min

We start by explaining why credit risk is important for financial institutions. We also define ground 0 terms, such as expected loss, probability of default, loss given default and exposure at default.

What does the course cover
5 min
What is credit risk and why is it important?
5 min
Expected loss (EL) and its components: PD, LGD and EAD
4 min
Capital adequacy, regulations, and the Basel II accord
5 min
Basel II approaches: SA, F-IRB, and A-IRB
10 min
Different facility types (asset classes) and credit risk modeling approaches
9 min
2. Setting up the environment

2 Lessons 2 Min

Here you will learn how to set up Python 3 and load up Jupyter. We’ll also show you what the Anaconda Prompt is and how you can use it to download and import new modules.

Setting up the environment Read now
1 min
Installing the relevant packages
1 min
3. Dataset description

2 Lessons 9 Min

Our example focuses on consumer loans. Since there are more than 100 potential features, we've devoted a complete section to explain why some features are chosen over others.

Our example: consumer loans. A first look at the dataset
3 min
Dependent variables and independent variables
6 min
4. General preprocessing

6 Lessons 29 Min

Each raw datasets has its drawbacks. While most preprocessing is model specific, in some cases (like missing values imputation), we could generalize the data preparation.

Importing the data into Python
4 min
Preprocessing few continuous variables
13 min
Preprocessing few continuous variables Homework Read now
1 min
Preprocessing few discrete variables
7 min
Check for missing values and clean
3 min
Check for missing values and clean Homework Read now
1 min
5. PD model: data preparation

18 Lessons 117 Min

Once we have completed all general preprocessing, we dive into model-specific preprocessing. We employ fine classing, coarse classing, weight of evidence and information value criterion to achieve the probability of default preprocessing. Conventionally, we should turn all variables into dummy indicators prior to modeling.

How is the PD model going to look like?
4 min
Dependent variable: Good/ Bad (default) definition
5 min
Constructing independent variables
6 min
Information value
5 min
Data preparation. Splitting data
8 min
Data preparation. Preprocessing one discrete variable
8 min
Data preparation. Preprocessing discrete variables: automating calculations
6 min
Data preparation. Preprocessing discrete variables: visualizing results
10 min
Data Preparation. Preprocessing Discrete Variables: Creating Dummies (part 1)
7 min
Data Preparation. Preprocessing Discrete Variables: Creating Dummies (part 2)
11 min
Data Preparation. Preprocessing Discrete Variables: Creating Dummies (part 2) Read now
1 min
Data preparation. Preprocessing continuous variables: automating calculations
5 min
Data preparation. Preprocessing continuous variables: creating dummies (part 1)
7 min
Data preparation. Preprocessing continuous variables: creating dummies (part 2)
14 min
Data preparation. Preprocessing continuous variables: creating dummies (part 2) Read now
2 min
Creating dummies Homework Read now
1 min
Data preparation. Preprocessing continuous variables: creating dummies (part 3)
13 min
Data preparation. Preprocessing the test dataset
4 min
6. PD model estimation

5 Lessons 35 Min

Having set up all variables to be dummies, we estimate the probability of default. The most intuitive and widely accepted approach is to employ a logistic regression.

The PD model. Logistic regression with dummy variables
8 min
Loading the data and selecting the features
6 min
PD model estimation
4 min
Build a logistic regression model with p-values.
11 min
Interpreting the coefficients in the PD model
6 min
7. PD model validation (test)

3 Lessons 28 Min

Since each model overfits the training data, it is crucial to test the results on out-of-sample observations. Consequently, we find its accuracy, its area under the curve (AUC), the Gini coefficient and the Kolmogorov-Smirnov test.

Out-of-sample validation (test).
7 min
Evaluation of model performance: accuracy and area under the curve (AUC)
11 min
Evaluation of model performance: Gini and Kolmogorov-Smirnov.
10 min
8. Applying the PD model for decision making

6 Lessons 37 Min

In practice, banks don't really want a complicated Python-implemented model. Instead, they prefer a simple score-card which contains only yes and no questions that could be employed by any bank employee. In this section, we learn how to create one.

Calculating probability of default for a single customer
5 min
Creating a scorecard
13 min
Calculating credit score
6 min
From credit score to PD
3 min
Setting cut-offs
9 min
Setting cut-offs Homework Read now
1 min
9. PD model monitoring

4 Lessons 29 Min

Model estimation is extremely important, but an often-neglected step is model maintenance. A common approach is to monitor the population stability over time using the population stability index (PSI) and revisit our model if needed.

PD model monitoring via assessing population stability
5 min
Population stability index: preprocessing
12 min
Population stability index: calculation and interpretation
11 min
Population stability index: calculation and interpretation Homework Read now
1 min
10. LGD and EAD models

3 Lessons 17 Min

To calculate the final expected loss, we need three ingredients: probability of default (PD), loss given default (LGD) and exposure at default (EAD). In this section, we preprocess our data to be able to estimate the LGD and EAD models.

LGD and EAD models: independent variables
6 min
LGD and EAD models: dependent variables
5 min
LGD and EAD models: distribution of recovery rates and credit conversion factors
6 min
11. LGD model

8 Lessons 29 Min

LGD models are often estimated using a beta regression. To keep the modeling part simpler, we employ a two-step regression model, which aims to simulate a beta regression. We combine the predictions from a logistic regression with those from a linear regression to estimate the loss given default.

LGD model: preparing the inputs
3 min
LGD model: testing the model
5 min
LGD model: estimating the accuracy of the model
5 min
LGD model: saving the model
3 min
LGD model: stage 2 – linear regression
4 min
LGD model: stage 2 – linear regression evaluation
4 min
LGD model: combining stage 1 and stage 2
3 min
LGD model: combining stage 1 and stage 2 Homework Read now
2 min
12. EAD model

3 Lessons 11 Min

The exposure at default (EAD) modeling is very similar to the LGD one. In this section, we take advantage of a linear regression to calculate EAD.

EAD model estimation and interpretation
6 min
EAD model validation Read now
1 min
EAD model validation
4 min
13. Calculating expected loss

2 Lessons 17 Min

After having calculated PD, LGD, and EAD, we reach the final step: computing expected loss (EL). This is also the number which is most interesting to C-level executives and is the finale of the credit risk modeling process.

Calculating expected loss Homework Read now
1 min
Calculating expected loss
16 min

Topics

TheoryPythonData AnalysisProgrammingCredit RiskLogistic RegressionData PreprocessingData AnalysisFinance SkillsIndustry Specialization

Tools & Technologies

Course Requirements

You need to complete an introduction to Python before taking this course
Basic skills in statistics, probability, and linear algebra are required
It is highly recommended to take the Machine Learning in Python course first
You will need to install the Anaconda package, which includes Jupyter Notebook

Who Should Take This Course?

Level of difficulty: Advanced

Aspiring data scientists
Current data scientists who are passionate about acquiring domain-specific knowledge in credit risk modeling

Exams and Certification

A 365 Data Science Course Certificate is an excellent addition to your LinkedIn profile—demonstrating your expertise and willingness to go the extra mile to accomplish your goals.

Meet Your Instructor

Nikolay Georgiev

Director of Data Science and Automation at

2 Courses

797 Reviews

17647 Students

Nikolay is a Director of Data Science and Automation at KBC Group. He has a solid background in marketing analytics, risk modeling, and research. A Master’s degree in Science and a Ph.D. in Economics and Business Administration have given Nikolay vast experience in the academic world. He spent over six years in the field of research at HEC Paris, BI Norwegian Business School, and the University of Texas at Austin, U.S. In addition, Nikolay has worked on numerous projects for Coca-Cola Hellenic and Shawbrook Bank (UK) that involved building highly accurate quantitative models and solutions for customer portfolio management, credit risk, social media marketing research, and psychological targeting.