Using all elements for variations
I saw a question about question 1, for which the answer was that we use variations when we do not use ALL the elements in the sample space as we might with permutations. But I just fact checked that with another source and it clarified that yes, actually, you can use all elements in the sample space for a variation. Instead, the clarification they gave for the main difference between permutations and variations is that in variations, repetition of an element in the sample space is allowed. Please be careful in how you phrase answers to questions so that it is not misleading, and so that you do not convey incorrect information.
Hey Stephanie,
Thank you for reaching out.
I agree that there are subtleties. Note the following formulae:
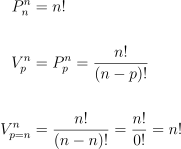
From the expressions above, you can see that all permutations are a type of variation (for which p = n). The difference between a permutation and a variation is that in a variation, it is not required to consider all elements in a set.
Note: Some probability textbooks don't even mention the term "variation" as a type of object arrangement. Instead, the authors use "permutations of p objects from n distinct objects" (as shown in the second expression).
Regarding your note on sets with repeating elements, you can find both the permutaions and variations of such sets. Variations with repetition are discussed in the lecture. Permutations with repetition obey the following formula, where there are "p" number of elements of one type, "q" number of elements of another type, "r" number of elements of a third type, etc.:
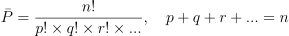
Hope this helps.
Kind regards,
365 Hristina