Why do we calculate z(1 -alfa/2) instead of z(1-alfa) if the z-table corresponds to z(1-alfa) and not z(1-alfa/2)
I would like to understand why in this lesson (time 5:16) we calculated z(1-alfa/2) = z(1-0,025 = 0,975) instead of z(1-alfa) = z(1-0,05 = 0,95).
The title of the z-table says "The table summarizes the standard normal distribution critical values and the corresponding ***(1-alfa)*** - and not (1-alfa/2) However, in the lecture we calculated z(1-alfa/2) and looked for the value of z(1-alfa/2)
The title of the z-table says "The table summarizes the standard normal distribution critical values and the corresponding ***(1-alfa)*** - and not (1-alfa/2) However, in the lecture we calculated z(1-alfa/2) and looked for the value of z(1-alfa/2)
2 answers ( 0 marked as helpful)
Hi there,
This depends on whether you need the probability on both sides or just one side of the mean.
In the case of confidence intervals, this is always on both sides.
Please check the z-table here: https://www.dropbox.com/s/j1iuhz7rrnw8ks7/3.9.The-z-table.xlsx?dl=0
Example 1 is the one you are looking for!
Best,
Iliya
Tiago, if you notice most Z Table charts provided online, there will be two charts. One is negative and one is positive Z Score. Why is this? Because as Iliya commented above, it depends on whether you need the probability on both sides or one side of the mean. The graphs below will help explain it better.
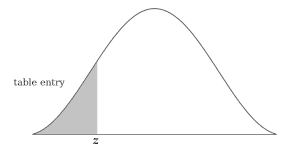
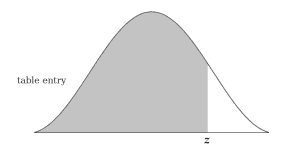Get the difference? Which is always on both sides in the case of confidence intervals. Hence we calculated z(1-alfa/2) = z(1-0,025 = 0,975) instead of z(1-alfa) = z(1-0,05 = 0,95). Please free to revert back if you need a longer explanation but I feel just looking at the graphs will simplify your doubts.
Have a good day! Hope this helps
Get the difference? Which is always on both sides in the case of confidence intervals. Hence we calculated z(1-alfa/2) = z(1-0,025 = 0,975) instead of z(1-alfa) = z(1-0,05 = 0,95). Please free to revert back if you need a longer explanation but I feel just looking at the graphs will simplify your doubts.
Have a good day! Hope this helps