Resolved: How is outer multiplication computed mathematically?
Hello,
I'm just having difficulty on understanding how outer multiplication works.
I create two matrices using the following objects:
mat.1 <- matrix(c(1, 2, -1, 1), nrow = 2)
mat.2 <- matrix(1:4, nrow = 2)
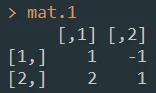

Now, when I try to use the outer multiplication, I get the result as the image below.
mat.outer <- mat.1 %o% mat.2
mat.outer

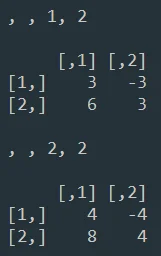
1. How did R computed the results?
2. Why did I get four matrices?
3. What does the dimensions " , , 1, 1", " , , 2, 1", " , , 1, 2", " , , 2, 2" mean for each result?
Kind regards,
Carl
Hi Carl,
thanks for reaching out! The exterior multiplication in R is something that's not the most typical matrix operation, so I'm glad you're asking this question.
What happens when you use mat.1 %o% mat.2 is that each value of your matrix mat.1 is multiplied by a scalar which is a value of mat.2. And in fact, your mat.1 is multiplied consequtevely with each value of mat.2 and the result is n new matrices, where n = mxl, where m and l are the dimensions of matrix m.
In your example you obtain 4 matrices. Each matrix is the result of multiplying mat.1 with a value from matrix 2. The dimensions you see
" , , 1, 1", " , , 2, 1", " , , 1, 2", " , , 2, 2"
show you which value from mat.2 you multiply with. So 1.1. means the first row and first column of your mat.2 - and the resulting first matrix is mat.1*[1].
Then "2,1,: means that you multiply your mat.1 with the value on the second row and first column of mat.2, so mat.1*[2]
and so on.
For exercise, you can check out these two matrices
A <- matrix(c(10, 8,
5, 12), ncol = 2, byrow = TRUE)
A
B <- matrix(c(5, 3,
15, 6), ncol = 2, byrow = TRUE)
B
A %o% B
and let me know if the results of the multiplication make sense.
Best,
365 Eli
I see, how could I've missed that scalar multiplication.
I got really confused with all the information I read in the internet. They always refer to inner and outer multiplication as the position of a row and column vectors in a dot product.
Really nice explanation and sample exercise.
Thanks Eli,
Carl