Hi, I have a question that after the np.log of y, why does that increase x by 1 unit, the transformed y increased by b1 percentage? Even for log10, the scaling is only 10 times but not 10 times? Also, for np.log, which is the nature log function rather than log10 function, does it affect the conclusion? Thank you. Best regards, Erica

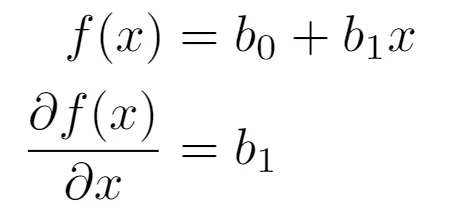
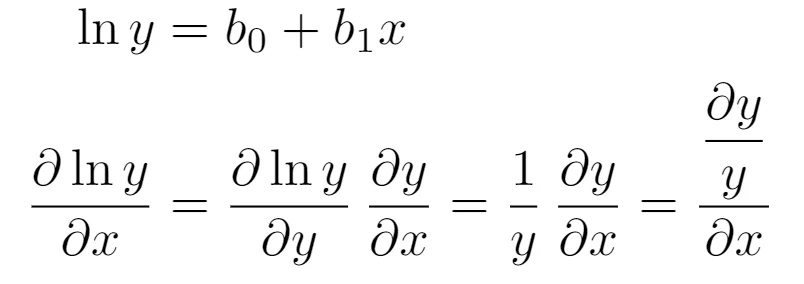
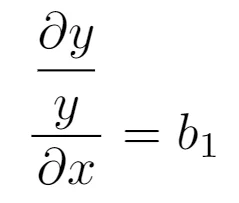
Hey Erica, Thank you for the great question! In order to give a complete answer, I need to employ a little bit of calculus. Suppose we have a function f(x), which bears the form given below. Let us take its derivative: Now, let us assume that f(x) = ln(y). Using the chain rule, its derivative is going to be: Now, we put the two derivatives equal to each other: The numerator on the left-hand side is the relative change in y - it is relative because we take the difference between two values of y (say, y_new - y_old) and know how this difference compares to y_old. 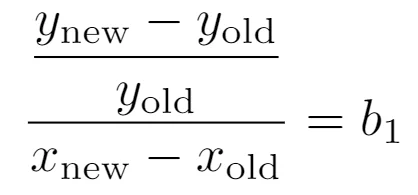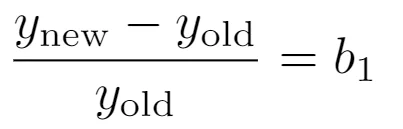The denominator is the absolute change in x: If we take the difference in x to be 1 (as suggested in the video), then: If we multiply the right-hand side of this equation by 100, then b1 will be converted into percentages. Therefore, an increase of 1 unit in x will result in an increase of b1 percent in y. To answer your second question - yes, it will make a difference whether we use natural logarithm or other bases. The reason is that the derivative of the logarithms having a basis different from e is no longer "one over the argument". However, a different basis will only scale the y-axis up or down - it won't change the overall form of the plot. I hope this answers your question! Unfortunately, the only way I could answer it is by making use of some mathematics. But regardless, the most important formula is actually the very last one :) Thank you and keep up the good work! Kind regards, 365 Hristina