Resolved: Question about the quiz after the lesson
I wonder why we have the same amount of options when we choose 5 types of macaroni and when we choose 3 of them? The formulas are:
For 5 types: 8!/(5!3!) = 56
For 3 types: 8!(3!5!) = 56
But for 4 types we have 8!/(4!4!) = 70
Dear Sali,
Thank you for your question!
What you are describing is a result of the symmetric nature of combinations. Choosing 3 flavors out of 8 and 5 flavors out of 8 is going to give you the same result. The reason is the following.
Let the total number of macaroon flavors be 8, that is n = 8. Let the number of flavors be k. Therefore, we can choose k = 3 and, as a consequence of this choice, n - k = 5 will be our "k-value" for the second case where the number of macaroons is 5. We can now write down the combinations formula for both cases. Using n and k (corresponding to 8 and 3) will give us the following:
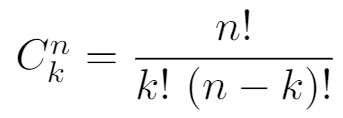
Using n and n-k (corresponding to 8 and 5) will, in turn, give us the following result:
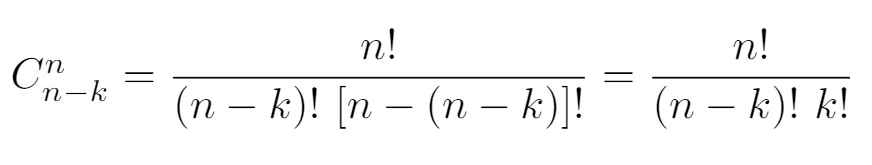
which is identical to the first result. Therefore, it is expected to obtain the same result for 3 and for 5 macaroons as 3 and 5 sum up to 8. This also means that you will get the same results for 2 macaroons and 6 macaroons (but this result will be different from the result for 3 and 5 macaroons). The same for 1 macaroon and 7 macaroons. Following this reasoning, there is only one case that will give 70 options, namely, 4 macaroons.
I hope this makes things clearer! :)
Kind regards,
365 Hristina