Most ML and AI libraries don’t require you to understand the math behind backpropagation to perform the process. TensorFlow, sklearn, and most other machine learning packages have incorporated backpropagation methods.
But knowing how it works will help you grasp the concept deeper and improve your performance of vanilla neural networks and ability to tackle more complex deep learning architectures.
This article breaks down backpropagation into its components and defines all concepts involved in the equations. It assumes a general understanding of neural networks and familiarity with backpropagation. Still, it recaps the basics and provides all necessary definitions to understand the backpropagation formulas.
The topics we touch on in this article are covered in detail in our Deep Learning with TensorFlow 2 course.
What Is Backpropagation?
The machine learning process is iterative. We feed data into the model and measure its accuracy through the objective function. Then, with the help of optimization algorithms, we vary the model’s parameters (weights and biases) until we reach the desired outputs. This comprises the training stage.
Forward propagation is the process of pushing inputs through the net. At the end of each epoch, we compare the obtained outputs to the targets to form the errors. In backpropagation, we reverse the process and adjust the weights and biases based on the obtained errors, minimizing the loss.
Backpropagation—short for ‘backward propagation of errors’—is an optimization algorithm used to improve the accuracy of artificial neural networks. It’s an essential component of the gradient descent optimization process.
Deep Neural Network Components
Before diving into the math behind backpropagation, we must understand deep neural networks’ components. In the following example, we provide several denotations in the computations below.
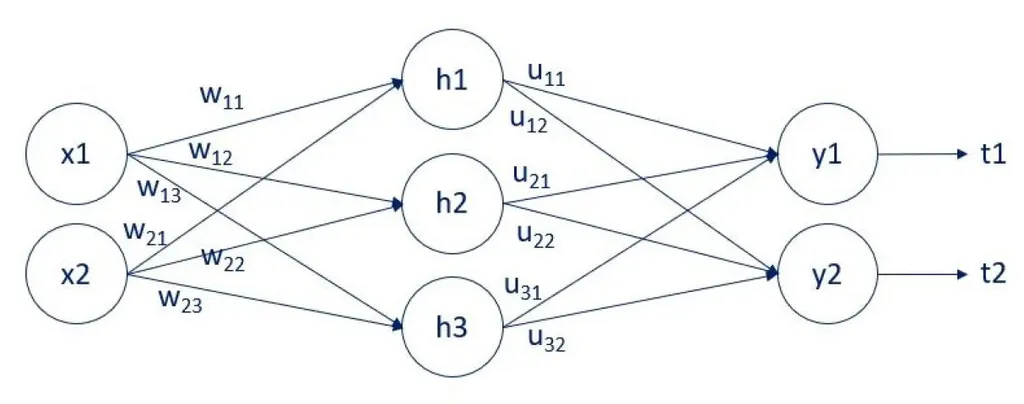
The deep neural network above contains an input layer, a hidden layer, and an output layer. It contains two inputs \( (x_1 \text{ and } x_2) \), three hidden units (nodes) \( (h_1, h_2, \text{ and } h_3) \), and two outputs \( (y_1 \text{ and } y_2) \).
The arrows that connect them are the weights (here, denoted by \( w \) and \( u \)). The \( w \) weights connect the input and the hidden layers. The \( u \) weights connect the hidden and the output layers. Lastly, we have the targets \( t_1 \) and \( t_2 \).
Backpropagation Concepts Explained
This section introduces key concepts and formulas to understand the more complex backpropagation computations below.
The Sigmoid Function
Deep neural networks are characterized by the existence of hidden layers, allowing us to represent complex relationships. And to stack layers, we need to add non-linearity (activation or transfer functions) to the weights. Activation functions transform inputs into outputs of a different kind. We cannot stack layers with linear relationships only.
Each arrow in the graphical representation above represents a mathematical transformation of a specific value or the linearly combined inputs with the added non-linearity to the weights in a neural network. In other words, we apply a given weight to the input, add non-linearity, and obtain the hidden layer’s units.
The sigmoid (logistic function) is one of the most common non-linearities. We represent it using the following equation.
\[ \sigma(x)=\frac{1}{1+e^{-x}} \]
The sigmoid’s derivative formula is the following:
\[ \sigma'(x) = \sigma(x)~(1-\sigma(x)) \]
The sigmoid activation function transforms the input values to obtain a new vector with values comprising the next layer.
The L-2 Norm
Objective functions are split into loss (cost) and reward functions. Here, we focus on loss functions, which measure the error of prediction.
The lower the cost function, the higher the model’s accuracy. So, we aim to minimize the error of prediction, and, consequently, the cost.
A typical loss function—used in supervised learning and, more concretely, regression—is the L2-norm or squared loss. The word ‘norm’ comes from ‘vector norm’—the Euclidean distance between the outputs and the targets.
We obtain this by calculating the sum of the squared differences between the outputs y and the targets t. Its mathematical expression is the following:
\[ \text{L2-norm loss: }L = \frac{1}{2}~\sum_i(y_i-t_i)^2 \]
Next, we examine the backpropagation algorithm for the output and hidden layers. We review them separately because the methodologies differ. But first, we must introduce a few more notations for the computations.
The linear model function equals:
f(x) = xw + b
where:
x – input
w – coefficient (weight)
b – intercept (bias)
Here, we’ll use a for the linear combination before activation, where:
\( a^{(1)} = xw + b^{(1)} \)
and
\( a^{(2)} = hu + b^{(2)} \)
With this notation, the output y equals the activated linear combination. Since we cannot exhaust all activation and loss functions, we focus on the most common ones: sigmoid activation and L2-norm loss. Therefore, for the output layer, we have \( y=\sigma\left( a^{(2)} \right) \), while for the hidden layer we obtain \( h=\sigma\left( a^{(1)} \right) \).
Backpropagation for the Output Layer
In supervised learning, the optimization process consists of minimizing the loss. The idea of backpropagation is to compute the gradient of the loss function concerning the weights and biases of each unit in the network. Then, we use the gradients obtained to update the parameters such that the loss we compute at the new value is less than the loss at the current value. The loss decreases by iteratively adjusting the weights and biases based on the obtained gradients, and the network gradually learns to make better predictions.
The updates are directly related to the partial derivatives of the loss and indirectly related to the errors or deltas—the differences between targets and outputs. Having these deltas allows us to modify the parameters using the update rule.
We obtain the update rule using the following function:
\[ \textbf{u} \leftarrow \textbf{u}-\eta\nabla_\textbf{u}L(\textbf{u}) \]
Where \( \eta \) (eta) is the ML algorithm's learning rate.
How do we calculate \( \nabla_\textbf{u}L(\textbf{u}) \)?
Let's take a single weight \( u_{ij} \). The partial derivative of the loss w.r.t. \( u_{ij} \) equals:
\[ \frac{\partial L}{\partial u_{ij}} = \frac{\partial L}{\partial y_j} ~ \frac{\partial y_j}{\partial a_j^{(2)}} ~ \frac{\partial a_j^{(2)}}{\partial u_{ij}} \]
Where:
i corresponds to the previous layer (input layer for this transformation) and
j corresponds to the next layer (output layer of the transformation).
We compute the partial derivatives following the chain rule.
The first one is the L2-norm loss derivative:
\[ \frac{\partial L}{\partial y_j} = (y_j - t_j) \]
The second one is the sigmoid derivative:
\[ \frac{\partial y_j}{\partial a_j^{(2)}} = \sigma\left( a_j^{(2)} \right) ~ \left( 1 - \sigma\left( a_j^{(2)} \right) \right) = y_j~(1-y_j) \]
Finally, the third one is the derivative of \( a^{(2)} = hu + b^{(2)} \), which equals:
\[ \frac{\partial a_j^{(2)}}{\partial u_{ij}} = h_i \]
Replacing the partial derivatives in the expression above, we get:
\[ \frac{\partial L}{\partial u_{ij}} = \frac{\partial L}{\partial y_j} ~ \frac{\partial y_j}{\partial a_j^{(2)}} ~ \frac{\partial a_j^{(2)}}{\partial u_{ij}} = (y_j-t_j)~y_j~(1-y_j)~h_i = \delta_j h_i \]
Therefore, we obtain the update rule for a single weight for the output layer using the following:
\[ u_{ij} \leftarrow u_{ij}-\eta~\delta_j~h_i \]
Backpropagation for a Hidden Layer
When working with deep neural networks, we must update the weights in several hidden layers. We must also consider the activation functions and update the weights in accordance with the used non-linearities and their derivates.
So, how does backpropagation work in this case?
Similarly to the backpropagation of the output layer, the update rule for a single weight, \( w_{ij} \), is the following:
\[ \frac{\partial L}{\partial w_{ij}} = \frac{\partial L}{\partial h_j} ~ \frac{\partial h_j}{\partial a_j^{(1)}} ~ \frac{\partial a_j^{(1)}}{\partial w_{ij}} \]
Again, we compute backpropagation following the chain rule.
We use the sigmoid activation and linear model formulas to obtain the following:
\[ \frac{\partial h_j}{\partial a_j^{(1)}} = \sigma\left( a_j^{(1)} \right) ~ \left( 1 - \sigma\left( a_j^{(1)} \right) \right) = h_j~(1-h_j) \]
and
\[ \frac{\partial a_j^{(1)}}{\partial w_{ij}} = x_i \]
But the calculation of the third component \( \frac{\partial L}{\partial h_{j}} \) is more complex.
The problem is that we don’t have targets for the hidden layers’ outputs, so we can’t calculate the deltas as we did for the output layers.
Instead, we solve this issue by tracing the contribution of each unit (hidden or not) to the outputs’ errors. Let’s illustrate this with the following backpropagation example.
Going back to the neural network above, we see that the weight \( u_{11} \) contributes to the output \( y_{1} \) and, respectively, to its error (let’s call it \( e_{1} \)). So, we can easily find its derivative and update the parameters.
But matters become more complicated when we get to the hidden layer. The weight \( w_{11} \) contributes to \( h_{1} \). But \( h_{1} \) is connected to the weights \( u_{11} \) and \( u_{12} \), contributing to two outputs. This means we can trace the contribution of \( w_{11} \) to two outputs (\( y_{1} \) and \( y_{2} \)) and errors (\( e_{1} \) and \( e_{2} \)).
How do we solve this problem?
We take the errors and backpropagate them through the net using the u weights. This allows us to measure the contribution of the hidden layers to the respective errors and use it to update the w weights.
Of course, this is a simplified explanation of the backpropagation algorithm for hidden layers. In the calculations, we must also account for non-linearities.
Let’s take the solution for weight \( w_{11} \) as an example:
\[ \frac{\partial L}{\partial h_1} = \frac{\partial L}{\partial y_1} ~ \frac{\partial y_1}{\partial a_1^{(2)}} ~ \frac{\partial a_1^{(2)}}{\partial h_{1}} + \frac{\partial L}{\partial y_2} ~ \frac{\partial y_2}{\partial a_2^{(2)}} ~ \frac{\partial a_2^{(2)}}{\partial h_{1}} =\]
\[ =(y_{1} - t_{1})y_{1}(1 - y_{1})u_{11} + (y_{2} - t_{2})y_{2}(1 - y_{2})u_{12} \]
Now, we can calculate \( \frac{\partial L}{\partial w_{11}} \), which was the only missing part of the update rule for the hidden layer. The final expression is:
\[ \frac{\partial L}{\partial w_{11}} = \left[ (y_1-t_1)~y_1~(1-y_1)~u_{11} + (y_2-t_2)~y_2~(1-y_2)~u_{12} \right]~h_1~(1-h_1)~x_1 \]
The generalized form of this equation is:
\[ \frac{\partial L}{\partial w_{ij}} = \sum_k (y_k-t_k)~y_k~(1-y_k)~u_{jk}~h_j~(1-h_j)~x_i \]
Backpropagation Generalization
We combine the backpropagation for the output and the hidden layers to obtain the general backpropagation formula with the L2-norm loss and sigmoid activations.
\[ \frac{\partial L}{\partial w_{ij}} = \delta_j~x_i \]
where for a hidden layer
\[ \delta_j = \sum_k \delta_k~w_{jk}~y_j~(1-y_j)~x_i \]
What’s Next?
Note that backpropagation is just one step in training a neural network. Other techniques and variations can be applied alongside it to enhance the process.
And while most ML and AI libraries don’t require you to know the formulas, understanding the math behind backpropagation helps you better grasp the concept.
If you wish to deepen your machine learning and deep learning knowledge, enroll in our Deep Learning with TensorFlow 2 course. You can try it for free by signing up for our program.






