Resolved: Z-statistic and t-statistic
What if the population variance is unknown and the sample is big. What statistic would we be using? Because from the exmaples illustrated - we use t-test for unknown and small and z-test for known and big
If the sample is bigger than 30 (n>30 for mean and n>15 for proportions) the CLT (central limit theorem) comes into play and you can use z-statistic. If you do not know the population variance, you use the sample variance.
Thank you for addressing my question. What do you mean by proportions in this context?
Sample Proportion. Just like sample mean. see the links below...
https://mathbitsnotebook.com/Algebra2/Statistics/STcompare.html
i dont agree with his answer because we only use CLT when we have many samples with different sizes so then we take mean for all of them and create a distribution of those means called sampling distribution and to answer your question we would use the z statistic.
So, to summarize:
If the population variance is known and the sample size is large or small, we can use a z-test.
If the population variance is unknown and the sample size is small (less than 30), we should use a t-test.
If the population variance is unknown and the sample size is large (greater than 30), we can use a z-test.
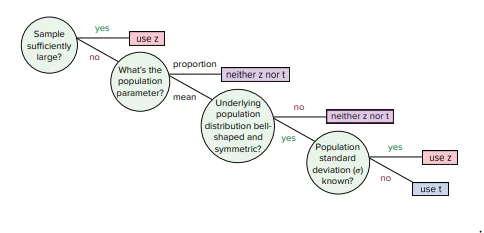
for small samples, you can follow this decision tree above, For larger samples CLT will apply so you can use z-statistic