If you have ever wondered if pizza in New York is cheaper than in LA, the measures of central tendency will provide the answer. This term may sound scary at first, but we are talking about mean, median and mode. Even if you are familiar with them, please stick around, as we will explore their upsides and shortfalls.
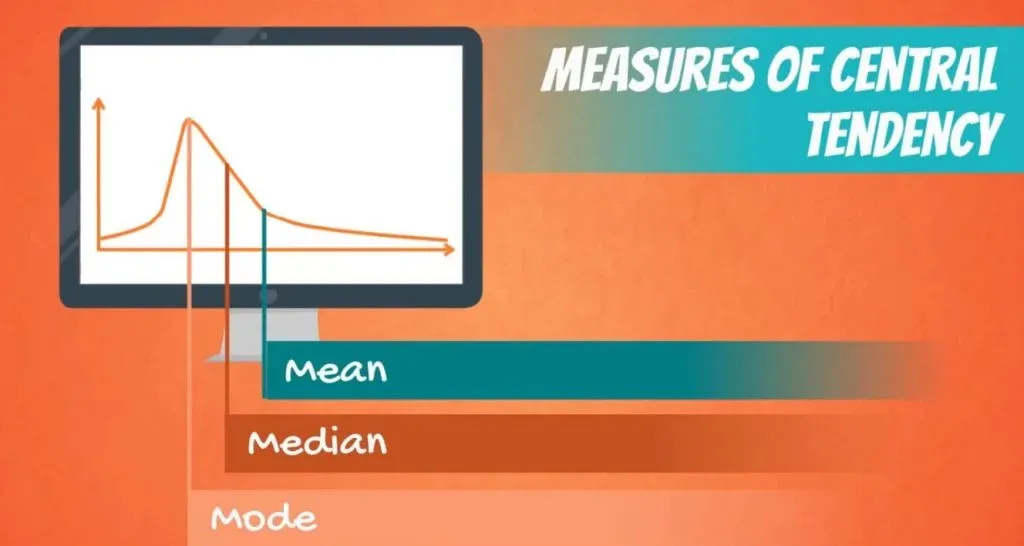
The Mean
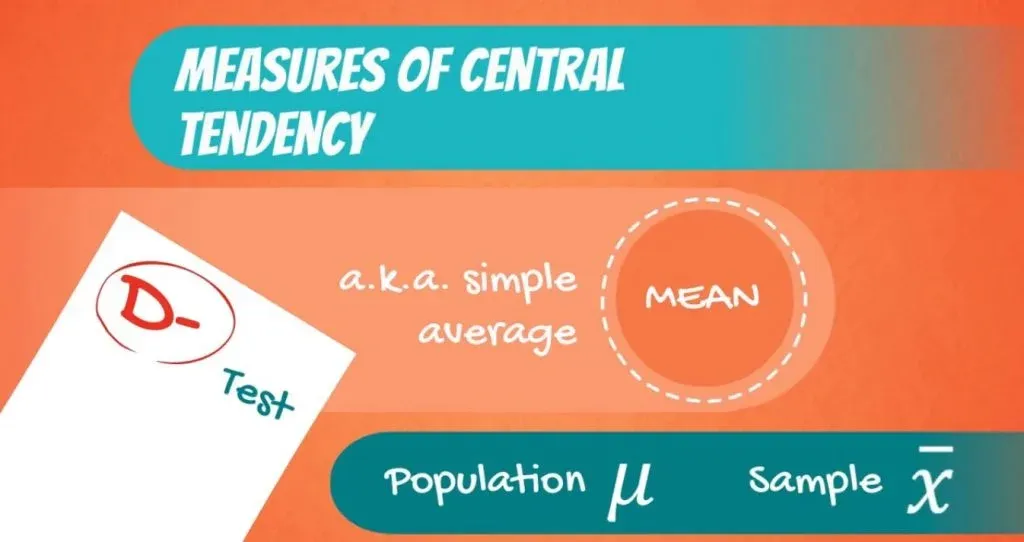
The first measure of central tendency which we will study is the mean, a.k.a. the simple average. It is denoted by the Greek letter m for a population and x_bar for a sample. You can see how they are denoted in the picture below.
These notions may come in handy as you go deeper into studying statistics.
We can find the mean of a data set by adding up all of its components and then dividing them by their number.
The Downside of the Mean
The mean is the most common measure of central tendency, but it has a huge downside – it is easily affected by outliers.
Let’s aid ourselves with an example.
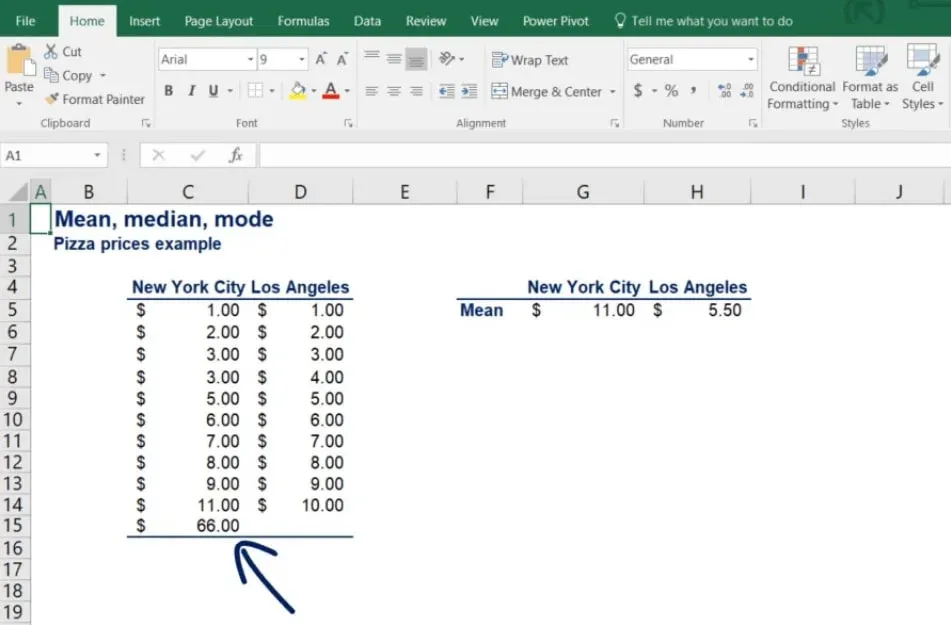
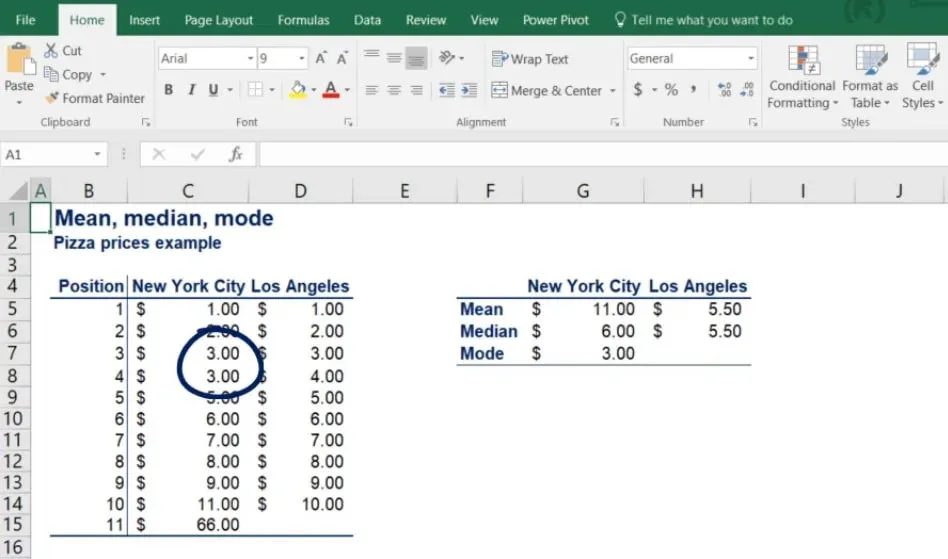
Take a look at the picture below.
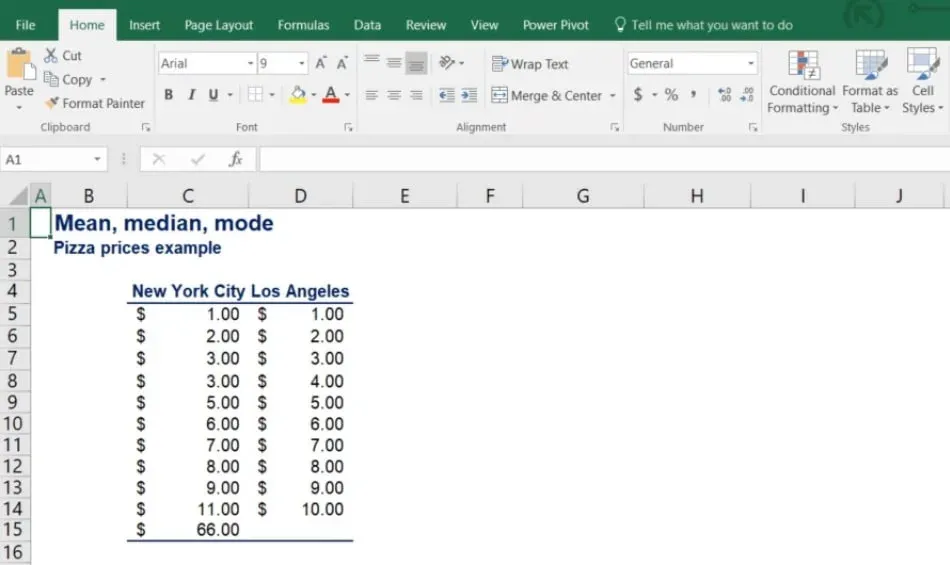
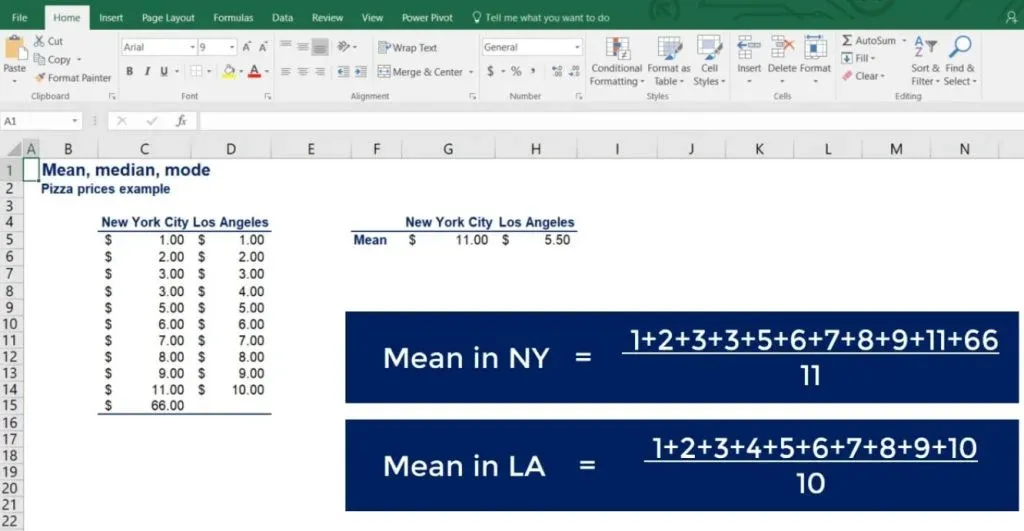
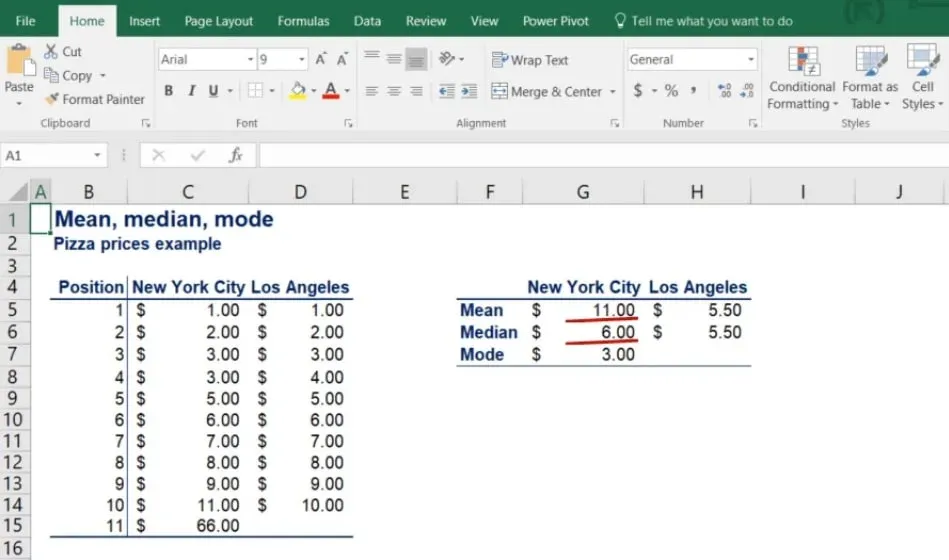
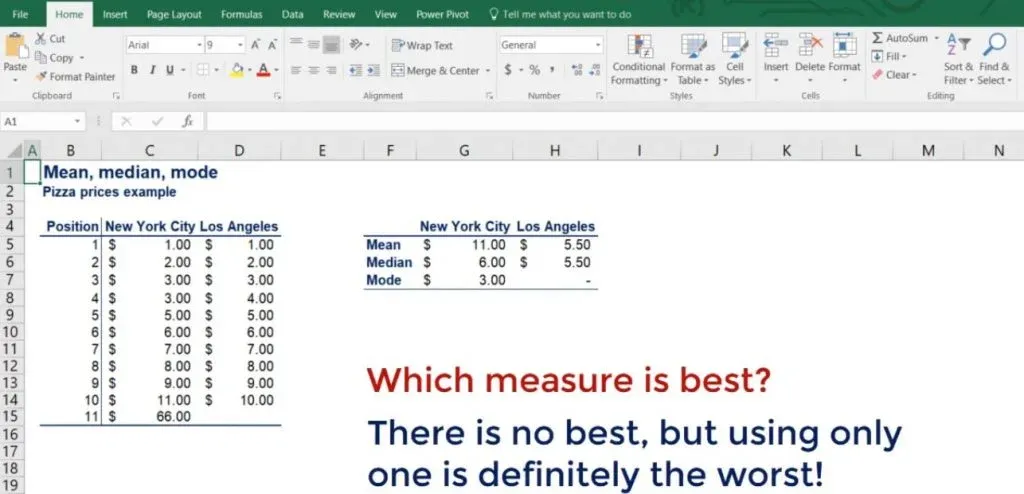
What you can see are the prices of pizza at 11 different locations in New York City and 10 different locations in LA. Let’s calculate the means of the two datasets using the formula.
For the mean in NYC, we get 11 dollars, whereas for LA - just 5.5! On average, there is no way that pizza in New York is twice as expensive as in LA.
The Problem
The problem is that in our sample, we have included one posh place in New York, where they charge 66 dollars for pizza.
This is what doubled the mean. What we should take away from this example is that the mean is not enough to make definite conclusions.
So, let’s find out how we can protect ourselves from this issue.
The Median
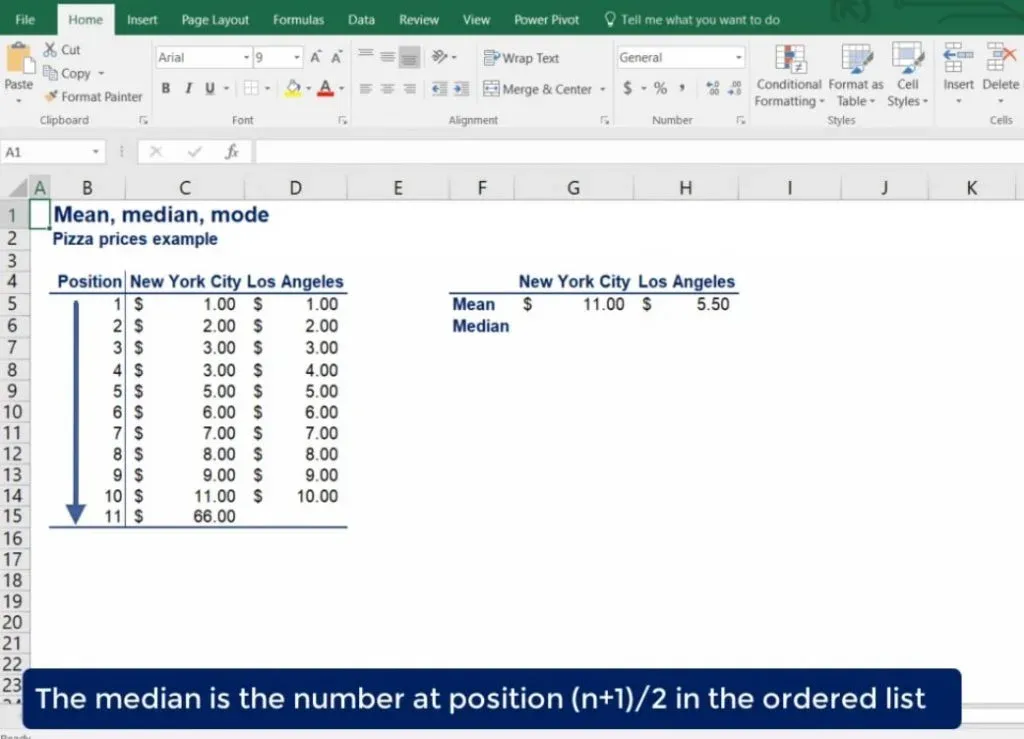
As you might have guessed, we can calculate the second measure – the median. The median is basically the ‘middle’ number in an ordered data set. Let’s see how it works for our example. In order to calculate the median, we have to order our data in ascending order.
The median of the data set is the number at position (n +1) / 2 in the ordered list, where n is the number of observations.
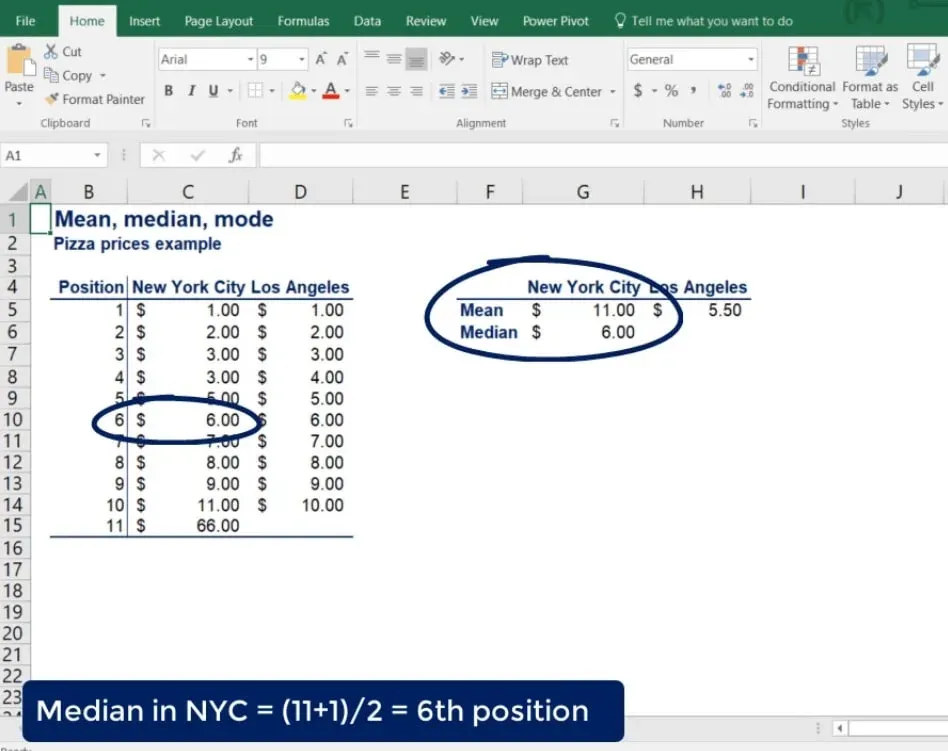
Therefore, the median for NYC is at the sixth position or $6. Much closer to the observed prices than the mean of $11.
A Particular Case
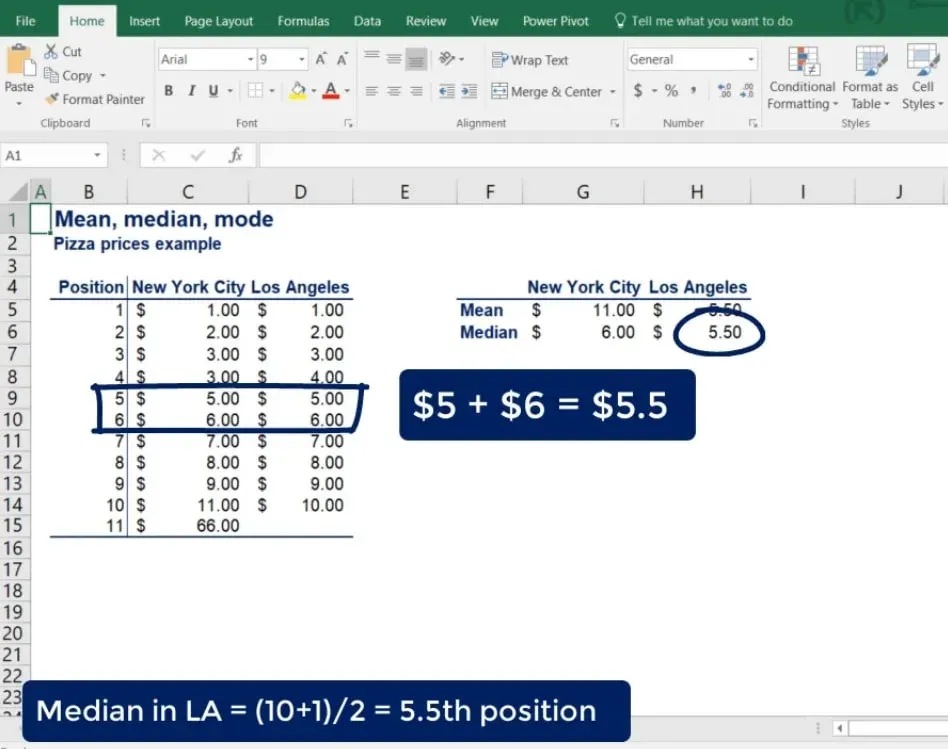
What about LA? We only have 10 observations there. According to our formula, the median is at position 5.5. In cases like this, the median is the simple average of the numbers at positions 5 and 6. Therefore, the median of LA prices is 5.5 dollars.
Now you know that the median is not affected by extreme prices, which is good when we have posh New York restaurants in a street pizza sample. But we still don’t get the full picture.
The Mode
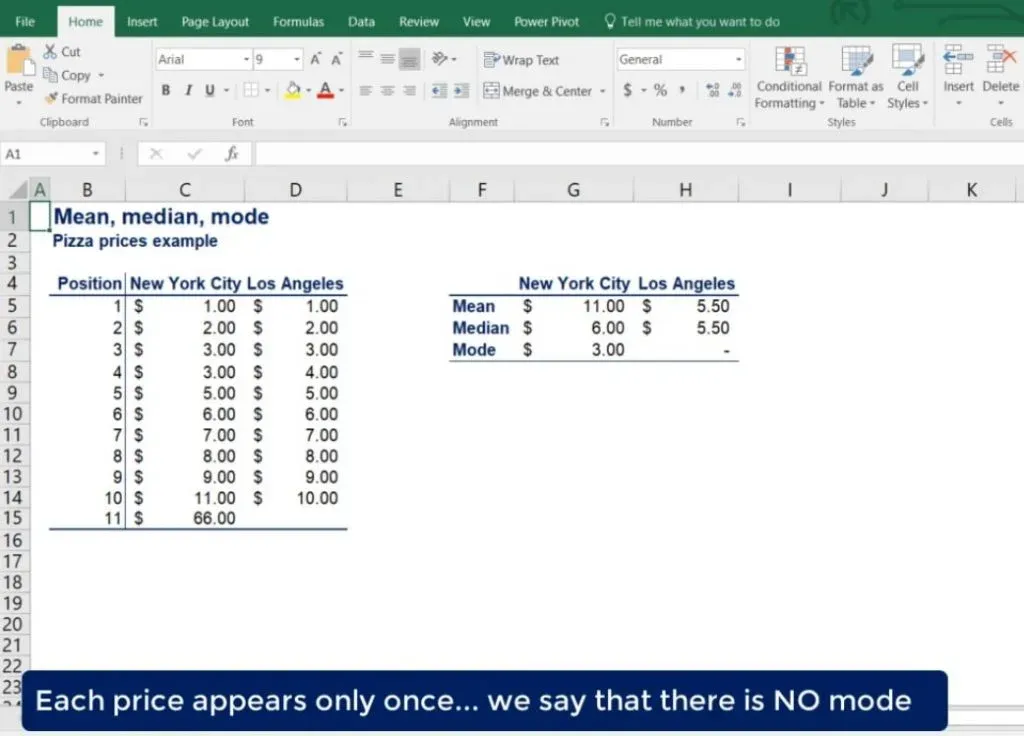
We must introduce another measure of central tendency – the mode. The mode is the value that occurs most often. It can be used for both numerical and categorical data, but we will stick to our numerical example. After counting the frequencies of each value, we find that the mode of New York pizza prices is 3 dollars.
Well, that’s interesting! The most common price of pizza in NYC is just 3 dollars, but the mean and median led us to believe it was much more expensive.
Another Interesting Case
Now, let’s do the same and find the mode of LA pizza prices. However, each price appears only once. How do we find the mode then? Well, we say that there is no mode.
You may be wondering if you can say that there are 10 modes. Sure you can, but it will be meaningless with 10 observations. Furthermore, an experienced statistician would never do that. In general, you often have multiple modes. Usually, two or three modes are tolerable, but more than that would defeat the purpose of finding a mode.
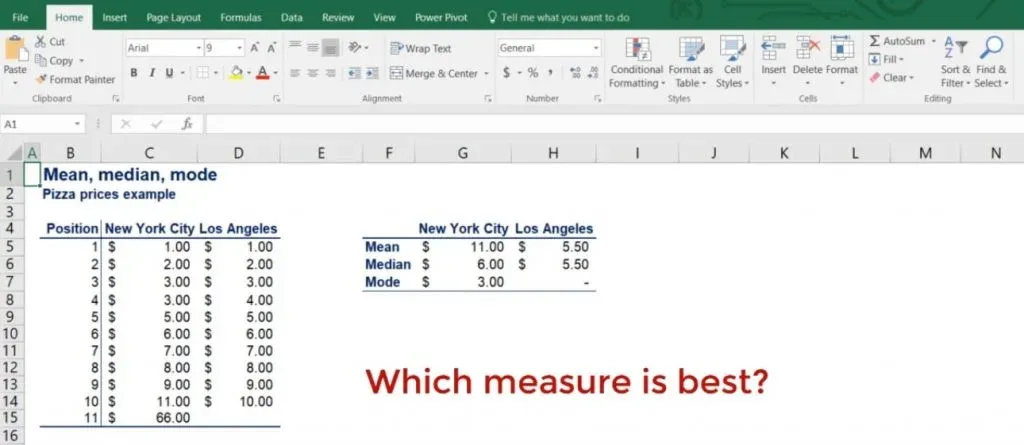
Which Measure of Central Tendency is the Best
This is the only question that we haven’t answered yet.
The NYC and LA example shows us that measures of central tendency should be used together rather than independently. Therefore, there is no best, but using only one is definitely the worst. Mostly, you'll need to estimate all of them and consider them jointly, which requires some time and effort.
To speed up the process, you can use our Mean, Median, Mode Calculator. It's an efficient and convenient way to obtain the results you need in just a few clicks.
In case you want to put what you’ve learned to practice, feel free to jump onto our tutorial about skewness.
***
Interested in learning more? You can take your skills from good to great with our statistics course! Try statistics course for free
Next Tutorial: Measuring Asymmetry with Skewness