Figuring out exactly what the null hypothesis and the alternative hypotheses are is not a walk in the park. Hypothesis testing is based on the knowledge that you can acquire by going over what we have previously covered about statistics in our blog.
So, if you don’t want to have a hard time keeping up, make sure you have read all the tutorials about confidence intervals, distributions, z-tables and t-tables.
We've also made a video on null hypothesis vs alternative hypothesis - you can watch it below or just scroll down if you prefer reading.
Confidence intervals provide us with an estimation of where the parameters are located. You can obtain them with our confidence interval calculator and learn more about them in the related article.
However, when we are making a decision, we need a yes or no answer. The correct approach, in this case, is to use a test.
Here we will start learning about one of the fundamental tasks in statistics - hypothesis testing!
The Hypothesis Testing Process
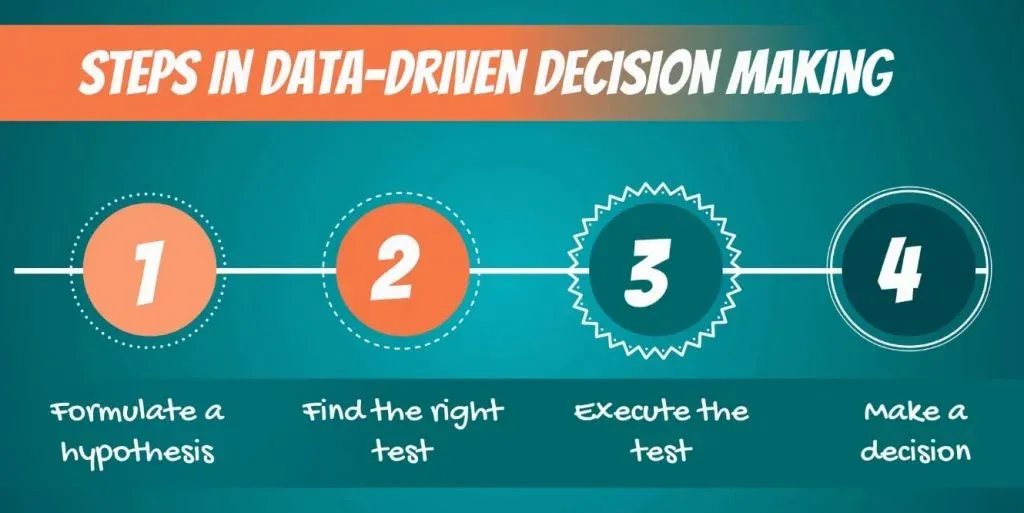
First off, let’s talk about data-driven decision-making. It consists of the following steps:
- First, we must formulate a hypothesis.
- After doing that, we have to find the right test for our hypothesis.
- Then, we execute the test.
- Finally, we make a decision based on the result.
Let’s start from the beginning.
What is a Hypothesis?
Though there are many ways to define it, the most intuitive must be:
“A hypothesis is an idea that can be tested.”
This is not the formal definition, but it explains the point very well.
So, if we say that apples in New York are expensive, this is an idea or a statement. However, it is not testable, until we have something to compare it with.
For instance, if we define expensive as: any price higher than $1.75 dollars per pound, then it immediately becomes a hypothesis.
What Cannot Be a Hypothesis?
An example may be: would the USA do better or worse under a Clinton administration, compared to a Trump administration? Statistically speaking, this is an idea, but there is no data to test it. Therefore, it cannot be a hypothesis of a statistical test.
Actually, it is more likely to be a topic of another discipline.
Conversely, in statistics, we may compare different US presidencies that have already been completed. For example, the Obama administration and the Bush administration, as we have data on both.
A Two-Sided Test
Alright, let’s get out of politics and get into hypotheses. Here’s a simple topic that CAN be tested.
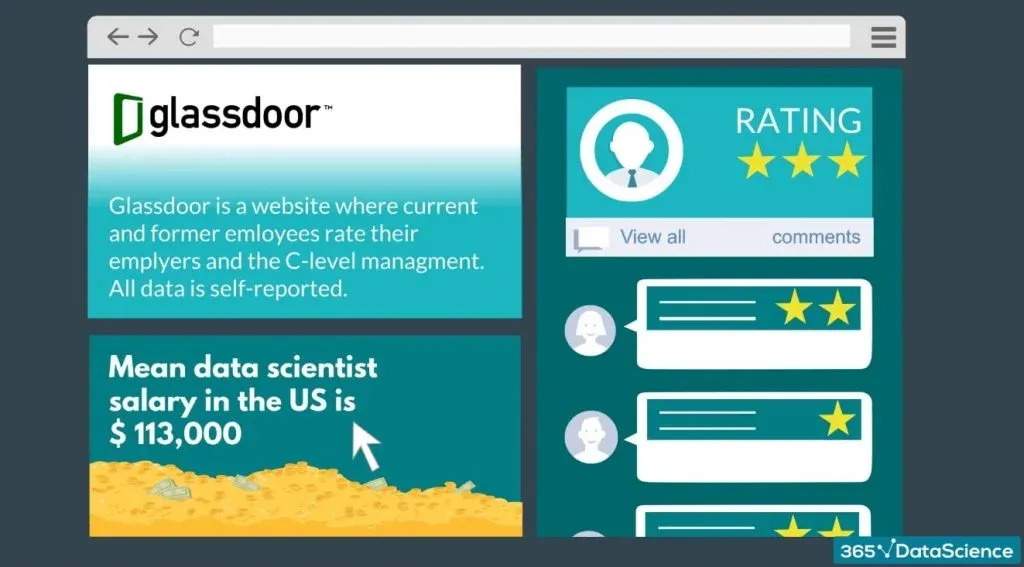
According to Glassdoor (the popular salary information website), the mean data scientist salary in the US is 113,000 dollars.
So, we want to test if their estimate is correct.
The Null and Alternative Hypotheses
There are two hypotheses that are made: the null hypothesis, denoted H0, and the alternative hypothesis, denoted H1or HA.
The null hypothesis is the one to be tested and the alternative is everything else. In our example:
The null hypothesis would be: The mean data scientist salary is 113,000 dollars.
While the alternative: The mean data scientist salary is not 113,000 dollars.
Author's note: If you're interested in a data scientist career, check out our articles Data Scientist Career Path, 5 Business Basics for Data Scientists, Data Science Interview Questions, and 15 Data Science Consulting Companies Hiring Now.
The Concept of the Null Hypothesis
Now, you would want to check if 113,000 is close enough to the true mean, predicted by our sample. In case it is, you would accept the null hypothesis. Otherwise, you would reject the null hypothesis.
The concept of the null hypothesis is similar to: innocent until proven guilty. We assume that the mean salary is 113,000 dollars and we try to prove otherwise.
This is called a two-sided or а two-tailed test.
An Example of a One-Sided Test
You can also form one-sided or one-tailed tests.
Say your friend, Paul, told you that he thinks data scientists earn more than 125,000 dollars per year. You doubt him, so you design a test to see who’s right.
The null hypothesis of this test would be: The mean data scientist salary is more than 125,000 dollars.
The alternative will cover everything else, thus: The mean data scientist salary is less than or equal to 125,000 dollars.
Important: The outcomes of tests refer to the population parameter rather than the sample statistic! So, the result that we get is for the population.
Important: Another crucial consideration is that, generally, the researcher is trying to reject the null hypothesis. Think about the null hypothesis as the status quo and the alternative as the change or innovation that challenges that status quo. In our example, Paul was representing the status quo, which we were challenging.
Let’s go over it once more. In statistics, the null hypothesis is the statement we are trying to reject. Therefore, the null hypothesis is the present state of affairs, while the alternative is our personal opinion.
Why Hypothesis Testing Works
Right now, you may be feeling a little puzzled. This is normal because this whole concept is counter-intuitive at the beginning. However, there is an extremely easy way to continue your journey of exploring it. By diving into the linked tutorial, you will find out why hypothesis testing actually works.
***
Interested in learning more? You can take your skills from good to great with our statistics course!
Try statistics course for free
Next Tutorial: Hypothesis Testing: Significance Level and Rejection Region