Bayesian vs frequentist inference and the pest of premature interpretation.
Brace yourselves, statisticians, the Bayesian vs frequentist inference is coming!
Consider the following statements.
- The bread and butter of science is statistical testing.
- It isn’t science unless it’s supported by data and results at an adequate alpha level.
- Statistical tests give indisputable results.
One of these is an imposter and isn’t valid. “Statistical tests give indisputable results.” This is certainly what I was ready to argue as a budding scientist. But the wisdom of time (and trial and error) has drilled it into my head that statistics is only a tool, and it’s up to the scientist to make the decisions that will determine the final result.
And in naive hands, statistics is a tool with the power to rig things up profoundly.
That said, I felt it’s my duty to revisit the topic of a not so well-known statistical phenomenon which illustrates just how much statistics is only a tool. To all aspiring and seasoned data scientists, I present to you: Lindley’s paradox.
Lindley’s paradox can be considered the battleground where Bayesian vs frequentist reasoning ostensibly clash. The paradox generally consists in testing a highly-defined H0 against a broad-termed H1 using a large, LARGE dataset, and observing that the frequentist approach strongly rejects the null, while the Bayesian method unequivocally supports accepting the same null... or vice versa.
Uh-oh.
But fear not, dear reader. Here’s how we’ll approach the problem:
- A quick refresher on Bayesian theory
- An intuitive example of Lindley’s paradox… with numbers and Greek letters
- “Is Lindley’s paradox a paradox?”: a discussion
- Implications for the data scientist
The ABCs of Bayesian theory
Meet Alex Soos. Alex is a bright little girl, aged 11. She wakes up one day and feels a strange tingling sensation in her stomach. It’s not quite as if she’s ill; she isn’t sure how to describe it. Like a bright yellow light in her stomach, maybe.
She goes to her parents and tells them, looking for an explanation. Mid-discussion the three of them are distracted by a faint tap on the kitchen window. It’s a dusty grey owl, and it’s looking right at Alex’s family.
‘Mum, dad, look, it has a letter on its leg!’ Alex chortles, almost forgetting the sensation in her stomach.
The letter states:

Alex starts to tremble all over.
‘Can this be true, Mum? Dad?’ she asks, terrified of the unknown future a magical identity holds.
Alex’s parents exchange meaningful looks. ‘Well’, Dad starts, a twinkle in his eye, ‘you’ve read the probability theory textbook Grandpa gave you for Christmas, you tell us.’
‘From what we know, wizardry is extremely rare in the general population. Only 0.1% of people have magical powers.’, Mum adds.
‘Furthermore, the Hogwarts letters reach the correct recipient 99% of the time. However, the remaining 1% of the time, these letters end up somewhere in the non-magical world, perplexing little girls and boys like yourself.’ Dad checks in again.
‘So, you mean to tell me that there is a 99% chance I am a witch?’ screams in indignation Alex.
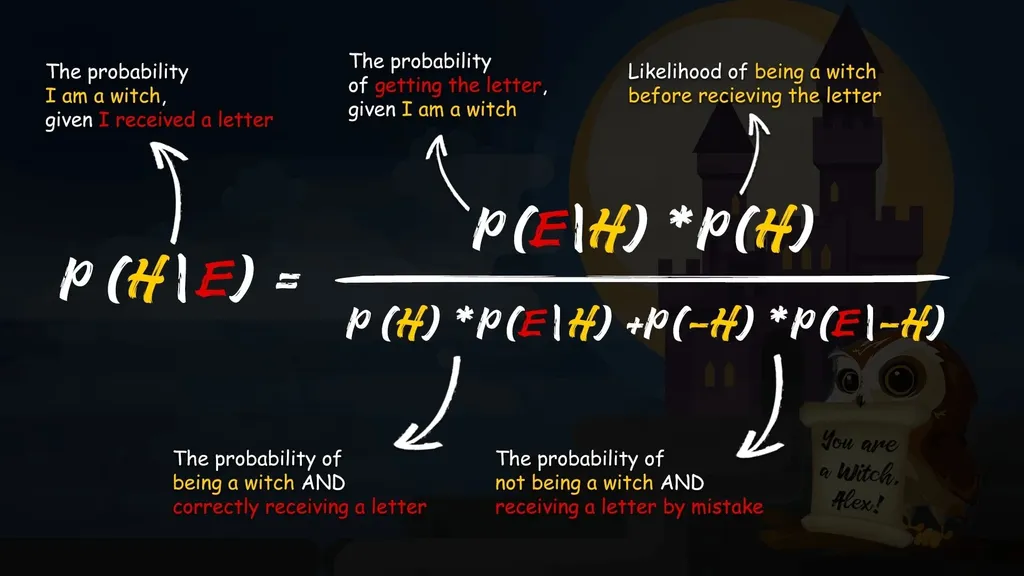
‘No, chicken, we just gave you the likelihoods, now you need to figure out the probability that you are a witch, given that you received a Hogwarts letter just now.’ Mum explains, patiently.
‘Oh… right. Okay. Bayes' theorem will give me the probability that a hypothesis is true, given an event.’
Alex recites the rule out of memory. ‘My hypothesis here is “I am a witch”, and the event: receiving the Hogwarts letter. So, the probability that I am a witch is conditional upon the probability of me receiving a letter.’ Alex’s parents are struck speechless. She is only 11! Alex, on the other hand, is blissfully unaware of her surroundings and deeply engaged with complex mental math.
‘To find out this probability, I need to take the prior probability of being magical (that is, the likelihood I am a witch before receiving the letter), and multiply that by the probability of the event, given the hypothesis is true (that is, the probability of getting the letter, given that I really am magical).’
‘Then’, Alex continues, ‘I need to divide all this by the probability of the event happening (that is, receiving the letter). To get there, I must calculate the probability of being magical and receiving the letter, and not being magical and receiving the letter by mistake. Right.’
Substituting these with the actual numbers gives Alex a much less confusing mental picture. Alex had read that figuring out the prior probability of things is the most difficult part, but in this case, it was easy: it’s the frequency of witches and wizards in the population, or 0.1%. And, since she already knew, because her parents had told her earlier, that the likelihood of a Hogwarts letter reaching the correct recipient is 99%, the rest was easy.
‘I guess the probability of being a witch, given the letter has been received, is 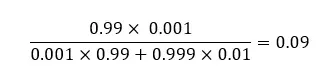
Bayesian vs frequentist: substituting the values
which amounts to a 9% chance.'
Odd.
‘So... the chance of me being a witch after receiving the letter is actually only 9%?’ Alex asks, surprised by the power of Bayesian inference to provide perspective.
‘Yep. So, no need to worry yet, chicken.’ Says Mum.
Cool. Now that we have the example ready, let’s snap back into the actual lesson of the article. Here are the key takeaways from the example.
First, what the numbers tell us makes sense. If Alex took 1000 people, only 1 would be a wizard and will have received their letter. Another 10, however, would have received a letter even though they are not magical. So, the chances Alex is a witch and has received her letter correctly are 1 in 11 (or 9%).
Second, if stripped down to its core, Bayes theorem is about updating our beliefs when new evidence becomes available. This means that it is best used many times: the more evidence, there is, the more accurately whatever result you get will reflect the state of things. Let me explain.
Some terminology: the posterior and the prior.
The posterior is what you are trying to determine. It is the probability of an event occurring after some evidence has been taken into account; like in the example, the probability Alex is a witch, given that she received a letter by owl. The posterior has a fun relationship with the prior. If new evidence comes into play, the last posterior you have becomes the new prior.
For example, if Alex were to receive a second letter reminding her she still hasn’t responded to the first one, the probability of Alex being a witch would look like this:
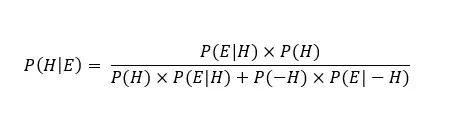
Bayesian vs frequentist: calculating the posterior
Substitute with the numbers, it looks like this:
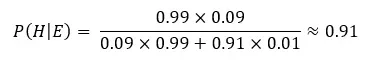
Bayesian vs frequentist: calculating the posterior
Did you notice that we used the probability of Alex being a witch which we determined when the first letter arrived as our prior, and calculated the new posterior probability of her being a witch, given that a second letter has arrived? Good noticing!
So, what’s the big deal about the prior?
The prior probability, or in our example the prior belief that Alex could be a witch before receiving the letter, is the initial degree of belief about the likelihood of an event, before considering the latest available evidence. The prior is kind of the powerhouse of Bayesian inference. Think of it this way: you are playing bowling, but you’re blindfolded. You release the ball and it hits the pins somewhere (in the middle, or towards the left edge, or towards the right). The point is, with each new release of the ball you get an increasingly more accurate representation of your initial bowl. In other words, you get an increasingly more informative posterior. And the prior? The prior is where you believe the ball hit, before each new release. It’s the last posterior you reached before considering the newest bowl.
This is all fairly straightforward. But...
Problems begin to arise when the previous posterior probability hasn’t been calculated
or isn’t known to the researcher, making setting a prior more difficult. This is where parameter estimation comes to the rescue. There are dozens of methods to estimate a prior. It’s beyond the scope of the article to review them, but I’ll just mention some of the most frequently used ones.
Use your understanding of the matter to propose a prior that is intuitive and reasonable.
This is a non-sophisticated approach but with careful sensibility and robustness analyses can yield reliable results.
Derive a non-informative prior, or use a prior distribution that is already available.
Non-informative priors are increasingly popular in Bayesian analysis. They provide an appearance of objectivity, as opposed to priors that are subjectively elicited. A non-informative prior gives a very general information about a variable; the best-known rule for determining a prior like this is the principle of indifference, where all possibilities are assigned equal probabilities. Remember this one, we’ll use it in a minute.
For a more in-depth discussion of non-informative priors, have a look at this passage, and this catalogue.
Wait. We can choose our own priors? But can’t this bias our results?
Absolutely. See, the beauty of Bayesian inference is that our actions play a role in determining the outcome and ultimately how we interpret the world. Sometimes, if you are an evil scientist, this also means you can use Bayesian inference to “lie with statistics”. (For a neat little way this happens in frequentists statistics, too, see Simpson's paradox).
Because Bayes’ theorem doesn’t tell us how to set our priors, paradoxes can happen.
If you'd like to learn more about Bayes' theorem, take our Machine Learning with Naive Bayes course that will teach you all the components of the Bayesian approach and how ti implement them in an ML setting.
Lindley’s paradox: the example
Now that we’ve brushed over our Bayesian knowledge, let’s see what this whole Bayesian vs frequentist debate is about. It’s time to dive into Lindley’s paradox.
Let’s say you are flipping a coin, and you have endless patience. You get 1,000,000 flips (N = 1,000,000), of which 498,800 are heads (k = 498,800), and 501,200 are tails (m = 501,200). You want to test whether the coin you’re using is fair. Coin flipping is a canonical binomial example, so we can assume that the number of times we got heads is a binomial variable (actually we are in the special case of the Bernoulli distribution). We can give it the parameter θ (you can also call it x, y, z, or Bob, if you want, it doesn’t matter). Your hypothesis is that the coins are unbiased, therefore θ = 0.5.
So, H0: The coins are fair.
H1: The coins are not fair.
And as any good statistician following the Bayesian method would, you will reject this hypothesis if statistical testing tells you the probability of the result is less than 5%. Similarly, following the frequentist school of thought, you would ask yourself “what is the probability of getting the number of tails I got, given θ = 0.5. If your result is less than 5%, you will again reject the null, that is, that the coins are fair. (You might also like our piece on Type I vs Type II errors and the importance of defining your H0 well.)
If you put your Bayesian statistician hat on for the analysis, you will need to define your prior.
As mentioned above, a non-informative prior can be considered the most objective option, so you do that. You define your prior to assign equal probabilities to all possibilities. So, it will be equally possible for θ = 0.5, and θ ≠ 0.5. In other words, the P(H0) = P(H1) = 0.5. Cool? Cool.
Then, the posterior probability of our hypothesis (H0) given the number of heads observed, is the following:
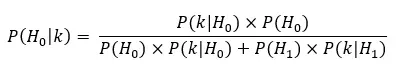
Bayesian vs frequentist: estimating coin flip probability with Bayesian inference
To get all the parameters, you need to calculate the P(k | H0) and P(k | H1), which can be done with a probability mass function for a binomial variable. The math looks like this:
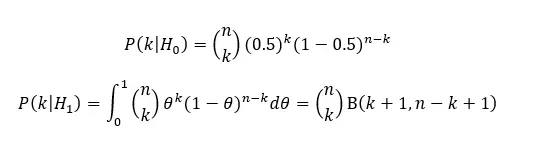
Bayesian vs frequentist: estimating coin flip probability with Bayesian inference
Don’t worry if not everything makes perfect sense, there is plenty of software ready to do the analysis for you, as long as it has the numbers, and the assumptions.
Finally, inputting all values into the equation, we get a posterior probability for H0 ≈ 0.98. This is an exceptionally large probability and it definitively supports H0: the coins are unbiased, and θ is indeed 0.5; the data is unequivocal.
Sweet.
Now, let’s do the same but while wearing our frequentist statistics hat.
Remember, the H0 is that θ = 0.5, and we reject it if there is less than 5% chance of getting the number of heads we got, given H0.
We assume the data are normally distributed because with a sample this big (N = 1,000,000) this is the natural assumption, following the central limit theorem.
The assumption of normality still holds, so we calculate a simple two-sided probability value, like this:
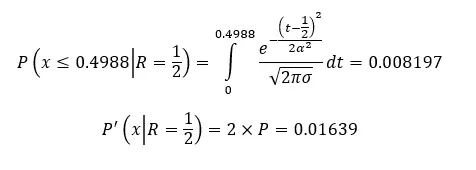
Bayesian vs frequentist: estimating coin flip probability with frequentist statistics
Oh, no. The p-value is highly significant. There is less than 2% probability to get the number of heads we got, under H0 (by chance). The frequentist scientist in you screams REJECT THE NULL, whereas the Bayesian theorist passionately urges you to ACCEPT THE NULL. The Bayesian vs frequentist clash in action!
While you stare at the results wide-eyed, Lindley’s paradox sniggers quietly in the dark.
But how – why – does this happen?
Lindley’s paradox explained
Lindley’s paradox can equally well be known as the paradox that isn’t a paradox at all. That’s right, Lindley’s paradox is a misnomer. Why?
Because the question that the Bayesian approach answers, and the one the frequentist approach answers, are different.
Do you remember how we defined the null? For H0 we chose θ = 0.5. We can agree that this is highly specific. On the other hand, for H1, or the alternative, we failed to provide any specification; we decided θ ≠ 0.5 sufficed. However, that means that θ can be anywhere in the [0,1] range.
The implications of this decision become clearer when you think of the posterior probabilities of P(k | H0) and P(k | H1) . How likely is it to see 498,800 heads in a 1,000,000 coin flips?
Under H0, θ assumes the value of 0.5.
Under H1, we choose θ to be any number between 0 and 1.
Now, the ratio of heads observed is 0.498. This is very close to the value of θ under the null. On the other hand, the majority of possible values for θ under the alternative hypothesis are far from 0.498. In other words, the data doesn’t support the diffuse alternative, in light of the tightly defined null. The posterior probability of P(k | H0) is a lot larger than the posterior probability of P(k | H1).
Alright, this explains why the Bayesian inference strongly favours the null.
But why does the frequentist method reject it?
At the core of the Bayesian vs frequentist problem is that the frequentist approach considers only the null. The probability test doesn’t make reference to the alternative hypothesis. Therefore, in essence, the frequentist approach only tells us that the null hypothesis isn’t a good explanation of the data, and stops there.
And that’s your answer!
While under the frequentist approach you get an answer that tells you H0 is a bad explanation of the data, under the Bayesian approach you are made aware that H0 is a much better explanation of the observations than the alternative.
See? Lindley’s paradox is no paradox at all, and the Bayesian vs frequentist clash isn’t really a clash – it just showcases how two methods answer different questions.
Implications of Lindley’s paradox for the data scientist
There are a couple of things I must point out about Lindley’s paradox.
First, the paradox in part arises because large data is oversensitive to very simple frequentist analysis, like rejecting a null. That said, it teaches us that large data is not the save-all messiah of statistical testing. Choosing the right statistics to calculate, and making the correct assumptions is.
Second, it is possible to sidestep Lindley’s paradox by defining a prior distribution that will yield the same results the frequentist approach does, but what will that teach us? The two methods – Bayesian vs frequentist – answer different questions, and are driven by different assumptions. As simple as that.
Again, if you want to become a successful data scientist, always think twice and three times what exactly you want to learn and whether your test will be adequate for answering your questions.
And finally, be wary of over specifying your hypotheses, and, conversely, making predictions that are too vague.
If Lindley’s paradox has taught us anything (okay, it teaches us many things), is that defining a hypothesis like this H0 = A, and the alternative as H1 ≠ A, is not good. What you are aiming to do is be in a state of balance: H0 = A, whereas H1 = B.
Okay, that’s Lindley’s paradox covered, the Bayesian vs frequentist reasoning refreshed on. Now that you warmed up your analytical reasoning, give our Simpson's paradox article a go.
Good reading, scientists!






