Time Series Analysis with Python

Curriculum

• Introduction Free

  1 Lesson 4 Min

  In this short section, we’ll tell you a bit more of what the course is about, how its structured and what our goal is.

  What does the Course Cover Free
• Setting Up the Environment Free

  2 Lessons 1 Min

  In this part of the course, we will explain to you how to set up Python 3 and then load up Jupyter. We’ll also show you what the Anaconda Prompt is and how we use it to download and import new modules.

  Setting up the Environment Free

  Installing the Necessary Packages Free
• Introduction to Time Series in Python Free

  7 Lessons 24 Min

  In this section of the course, we are going to learn what makes a dataset a time series, and discuss what separates it from cross-sectional data. We’ll introduce the appropriate mathematical notation for such data before loading up a dataset and quickly examining it.

  Introduction to Time Series Data Free

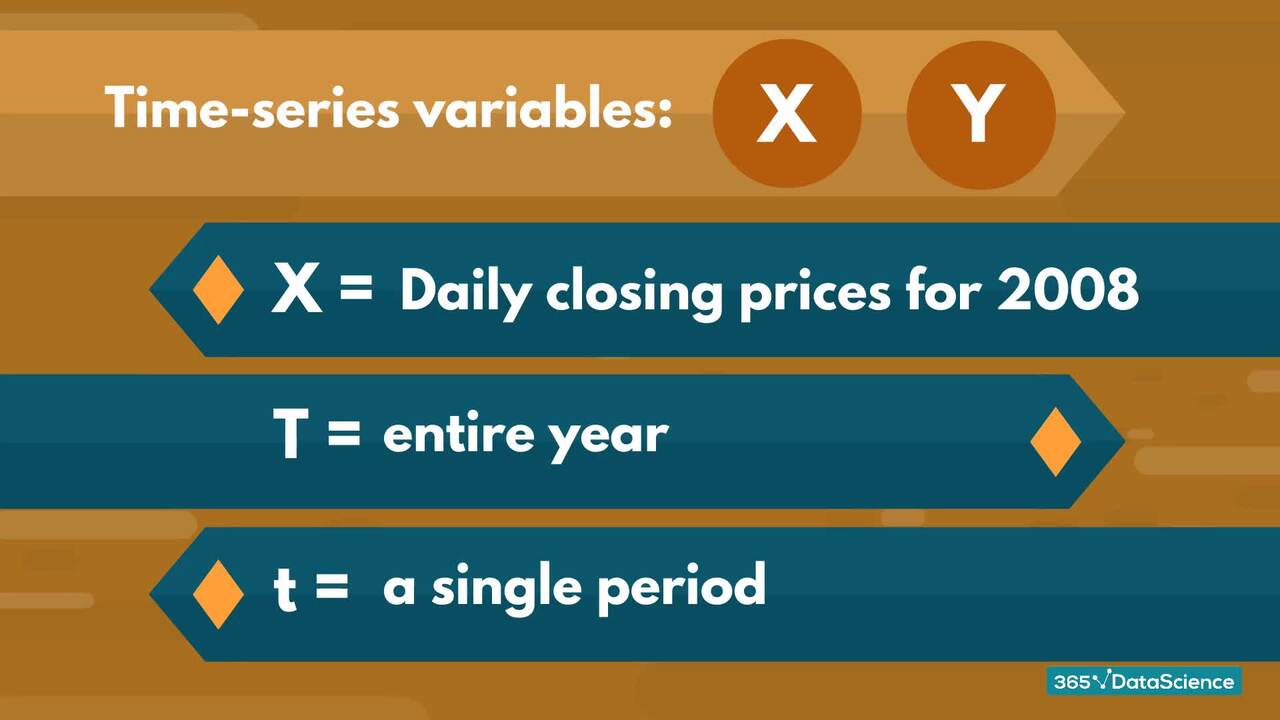
  Notation for Time Series Data Free

  Peculiarities of Time Series Data Free

  Loading the Data Free

  Examining the Data Free

  Plotting the Data Free

  The QQ Plot Free
• Creating a Time Series Object in Python

  7 Lessons 25 Min

  In this section of the course, we will go through the pre-processing aspects of working with time series. We’ll see how to interpret string text as dates and set these dates as indices of the data set. We’ll then set a fixed frequency and account for any missing values before splitting up the set for training and testing. In the appendix, we’ll show you how to import data directly from Yahoo Finance, so you can conduct your own analysis after completing the course.

  Transforming String Inputs into Date Time Values

  Using Dates as Indices

  Setting the Frequency

  Filling Missing Values

  Adding and Removing Columns in a Data Frame

  Splitting the Data

  Updating the Dataset
• Working with Time Series in Python

  8 Lessons 40 Min

  In this section of the course, we’ll examine and visualize some important types of time series, like white noise and a random walk. We’ll then discuss important concepts like stationarity, seasonality and autocorrelation, before exploring the ACF and PACF of a S&P 500’s prices.

  White Noise

  Random Walk

  Stationarity

  Determining Weak Form Stationarity

  Seasonality

  Correlation Between Past and Present Values

  The ACF

  The PACF
• Picking the Correct Model

  1 Lesson 3 Min

  In this short section, we’ll discuss the general rules of manual model selection. We will talk about which models we prefer, what we want to avoid and how to decide between models. We’ll talk about the Log-likelihood and information criterion as measurements of preference among similar models.

  Picking the Correct Model
• The AR Model

  12 Lessons 54 Min

  In this section, we’ll introduce the Autoregressive Model and see how well it models market index prices and returns. We’ll discuss how to use the PACF to determine the appropriate number of lags for the model and explore the concept of normalizing values and its impact on model selection.

  The AR Model

  Examining the ACF and PACF of Prices

  Fitting an AR(1) Model for Index Prices

  Fitting Higher-Lag AR Models for Prices

  Using Returns

  Examining the ACF and PACF of Returns

  Fitting an AR(1) Model for Returns

  Fitting Higher-Lag AR Models for Returns

  Normalizing Values

  Model Selection for Normalized Returns (AR Model)

  Examining the AR Model Residuals

  Unexpected Shocks from Past Periods
• The MA Model

  7 Lessons 34 Min

  In this section, we’ll introduce the Moving Average model and see how well it describes price returns. We’ll also have a look at how the MA model performs when dealing with non-stationary data and comment on the mathematical arguments for and against using such models for index prices.

  The MA Model

  Fitting an MA(1) Model for Returns

  Fitting Higher-Lag MA Models for Returns

  Examining the MA Model Residuals for Returns

  Model Selection for Normalized Returns (MA Model)

  Fitting an MA(1) Model for Prices

  Past Values and Past Errors
• The ARMA Model

  8 Lessons 41 Min

  In this section, we’ll combine the two models we just examined – the AR and MA – into one: the ARMA. We’ll examine how they synergize and limit the drawbacks each model has on its own. We’ll then talk about the issues that come along with finding the best-fitting ARMA model and see how checking the model residuals can be beneficial in model selection.

  The ARMA Model

  Fitting a Simple ARMA Model for Returns

  Fitting Higher-Lag ARMA Models for Returns - Part 1

  Fitting Higher-Lag ARMA Models for Returns - Part 2

  Fitting Higher-Lag ARMA Models for Returns - Part 3

  Examining the ARMA Model Residuals of Returns

  ARMA for Prices

  ARMA Models and Non-Stationary Data
• The ARIMA Model

  9 Lessons 45 Min

  In this section of the course, we’ll talk about “integration” and integrated models. We’ll explain why and when we use them, as well as when we should avoid them. Here, we’ll also briefly explain the idea of “MAX” models and how to add exogenous variables to any time series model.

  The ARIMA Model

  Fitting a Simple ARIMA Model for Prices

  Fitting Higher-Lag ARIMA Models for Prices - Part 1

  Fitting Higher-Lag ARIMA Models for Prices - Part 2

  Higher Levels of Integration

  Using ARIMA Models for Returns

  Outside Factors and the ARIMAX Model

  Seasonal Models - SARIMAX

  Predicting Stability
• The ARCH Model

  7 Lessons 34 Min

  In this section, we’ll talk about the idea of measuring volatility when we’re looking for stability in our investments. We’ll explain the multiple layers of ARCH models and how they differ from the ARMA family of models we just examined. We’ll spend some time discussing the vast functionality of the “arch_model” method and why it’s important to know the default values for many of its arguments.

  The ARCH Model

  Volatility

  A More Detailed Look of the ARCH Model

  The arhc_model Method

  The Simple ARCH Model

  Higher-Lag ARCH Models

  An ARMA Equivalent of the ARCH Model
• The GARCH Model

  5 Lessons 13 Min

  In this section of the course, we’ll discuss the generalized version of the ARCH model, also known as the GARCH. We’ll explore why this model is more widely used, how it outperforms high-order ARCH models and why it looks so similar to the ARMA. We’ll then empirically test the known fact that the GARCH(1,1) is the best model for measuring the volatility of price returns.

  The GARCH Model

  The ARMA and the GARCH

  The Simple GARCH Model

  Higher-Lag GARCH Models

  An Alternative to the Model Selection Process
• Auto ARIMA

  6 Lessons 28 Min

  In this section of the course, we’ll automate the model selection process with the help of the AUTO ARIMA package.

  Auto ARIMA

  Preparing Python for Model Selection

  The Default Best Fit

  Basic Auto ARIMA Arguments

  Advanced Auto ARIMA Arguments

  The Goal Behind Modelling
• Time Series Forecasting

  8 Lessons 46 Min

  In this section of the course, we will make forecasts about the future based on the simple models we have introduced so far.

  Introduction to Time Series Forecasting

  Simple Forecasting Returns with AR and MA

  Intermediate (MAX Model) Forecasting

  Advanced (Seasonal) Forecasting

  Auto ARIMA Forecasting

  Pitfalls of Forecasting

  Forecasting Volatility

  Appendix: Multivariate Forecasting (VARMAX)
• Business Case

  1 Lesson 28 Min

  In this final part of the course, we will examine how a real-life event like the Dieselgate scandal can alter the trends in time series data.

  Business Case - A Look Into the Automobile Industry